I’m very happy to announce that my paper with Rebecca Thornton, “Making the Grade: The Sensitivity of Education Program Effectiveness to Input Choices and Outcome Measures”, has been accepted by the Review of Economics and Statistics. An un-gated copy of the final pre-print is available here.
Here’s the abstract of the paper:
This paper demonstrates the acute sensitivity of education program effectiveness to the choices of inputs and outcome measures, using a randomized evaluation of a mother-tongue literacy program. The program raises reading scores by 0.64SDs and writing scores by 0.45SDs. A reduced-cost version instead yields statistically-insignificant reading gains and some large negative effects (-0.33SDs) on advanced writing. We combine a conceptual model of education production with detailed classroom observations to examine the mechanisms driving the results; we show they could be driven by the program initially lowering productivity before raising it, and potentially by missing complementary inputs in the reduced-cost version.
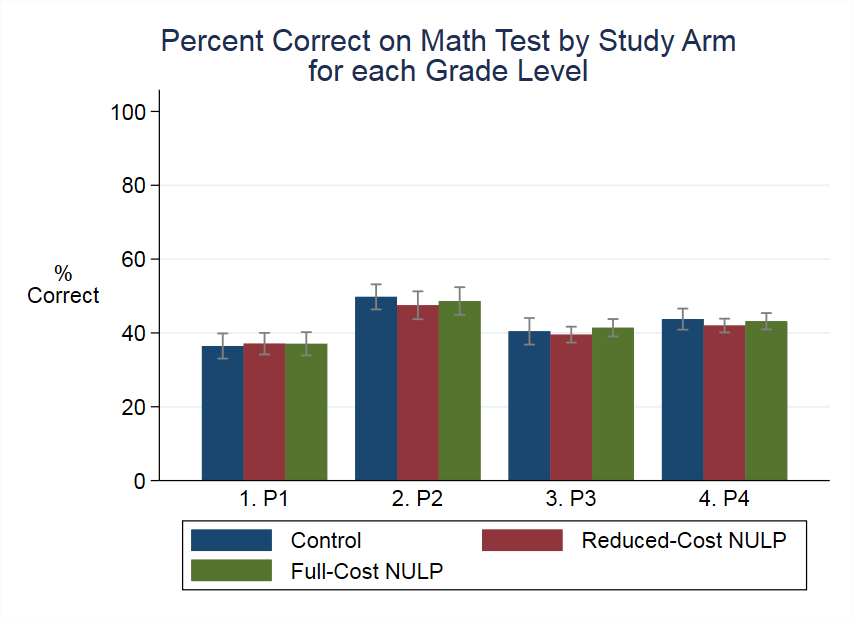
The program we study, the Northern Uganda Literacy Project, is one of the most effective education interventions in the world. It is at the 99th percentile of the distribution of treatment effects in McEwan (2015), and would rank as the single most effective for improving reading. It improves reading scores by 0.64 standard deviations. Using the Evans and Yuan equivalent-years-of-schooling conversion, that is as much as we’d expect students to improve in three years of school under the status quo. It is over four times as much as the control-group students improve from the beginning to the end of the school year in our study.
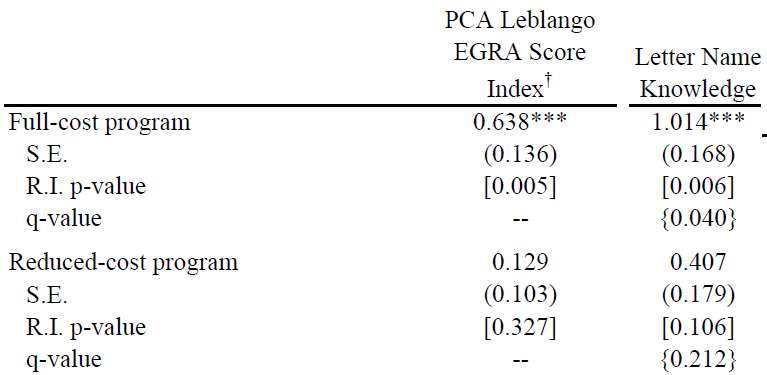
It is also expensive: it costs nearly $20 per student, more than twice as much as the average intervention for which cost data is available. So we worked with Mango Tree, the organization that developed it, to design a reduced-cost version. This version cut costs by getting rid of less-essential materials, and also by shifting to a train-the-trainers model of program delivery. It was somewhat less effective for improving reading scores (see above), and for the basic writing skill of name-writing, but actually backfired for some measures of writing skills:
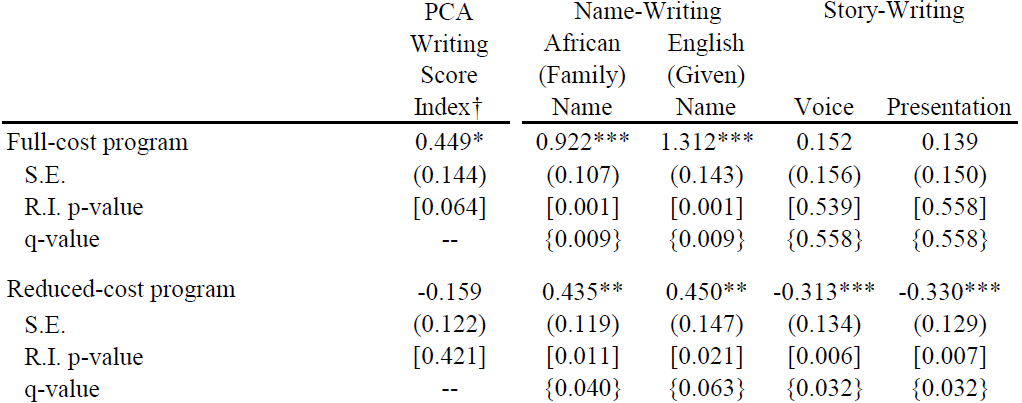
This means that the relative cost-effectiveness of the two versions of the program is highly sensitive to which outcome measure we use. Focusing just on the most-basic skill of letter name recognition makes the cheaper version look great—but its cost effectiveness is negative when we look at writing skills.
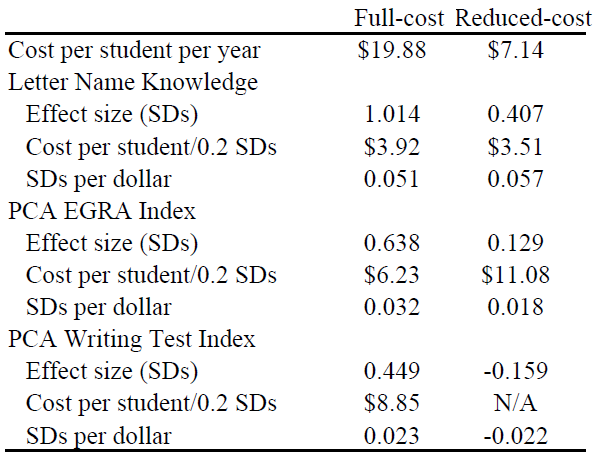
Why did this happen? The intervention was delivered as a package, and we couldn’t test the components separately for two reasons. Resource constraints meant that we didn’t have enough schools to test all the many different combinations of inputs. More important, practical constraints make it hard to separate some inputs from one another. For example, the intervention involves intensive teacher training and support. That training relies on the textbooks, and could not be delivered without them.
Instead, we develop a model of education production with multiple inputs and outputs, and show that there are several mechanisms that could lead to a reduction in inputs not just lowering the treatment effects of the program, but actually leading to declines in some education outcomes. First, if the intervention raises productivity more for one outcome more than another, this can lead to a decline in the second outcome due to a substitution effect. Second, a similar pattern can occur if inputs are complements in producing certain skills and one is omitted. Third, the program may actually make teachers less productive in the short term, as part of overhauling their teaching methods—a so-called “J-curve”.
We find the strongest evidence for this third mechanism. Productivity for writing, in terms of learning gains per minute, actually falls in the reduced-cost schools. It is plausible that the reduced-cost version of the program pushed teachers onto the negative portion of the J-curve, but didn’t do enough to get them into the region of gains. In contrast, for reading (and for both skills in the full-cost version) the program provided a sufficient push to achieve gains.
There is also some evidence of that missing complementary inputs were important for the backfiring of the reduced-cost program. Some of the omitted inputs are designed to be complements—for example, slates that students can use to practice writing with chalk. Moreover, we find that classroom behaviors by teachers and students have little predictive power for test scores when entered linearly, but allowing for non-linear terms and interactions leads to a much higher R-squared. Notably, the machine-learning methods we apply indicate that the greatest predictive power comes from interactions between variables.
These findings are an important cautionary tale for policymakers who are interested in using successful education programs, but worried about their costs. Cutting costs by stripping out inputs may not just reduce a program’s effectiveness, but actually make it worse than doing nothing at all.
For more details, check out the paper here. Comments are welcome—while this paper is already published, Rebecca and I (along with Julie Buhl-Wiggers and Jeff Smith) are working on a number of followup papers based on the same dataset.