There is a lot of writing advice out there and most of it is bad. Even worse, much writing advice is totally inapplicable to empirical science writing. Considering that, it’s entirely likely that this advice will be bad as well. Thus—as with all advice—you should feel free to exercise free disposal on what follows. But it’s what I teach my students and it works for many of them.
Economics is not a “write a lot of words” discipline. At the margin it’s better to have more papers, but all else equal a shorter paper is better and quality matters much more than quantity.
It’s easy to let yourself get psyched out by having to Write A Paper (or, even worse, having to Write A Dissertation). A common suggestion for overcoming that mental barrier is the “just write a bad draft quickly and then fix it later” strategy. A common suggestion is that you should just let the words flow out of you, forcing yourself to write lots, and then do a ton of editing after the fact. That might be great in fields where you need to churn out tons of pages, but economics is not like that (and quantitative science is generally not like that either, or at least it shouldn’t be). Another related strategy is to set goals of writing X hundred words per day, or to force yourself to write words for blocks of Y minutes at a time. None of this is conducive to our goal as social scientists, which is to communicate specific things to our audience rather than to flood the zone with tons of content.
Writing an applied microeconomics paper can be broken into the following manageable steps. Other than steps 1 and 3 you can do all the rest in 1 week apiece.
Here are the steps:
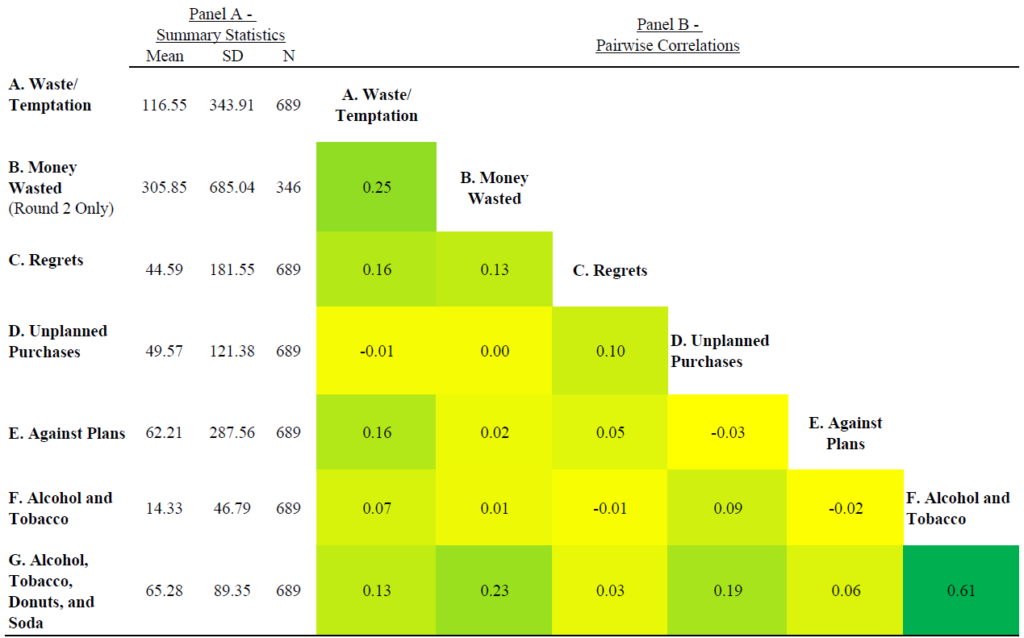
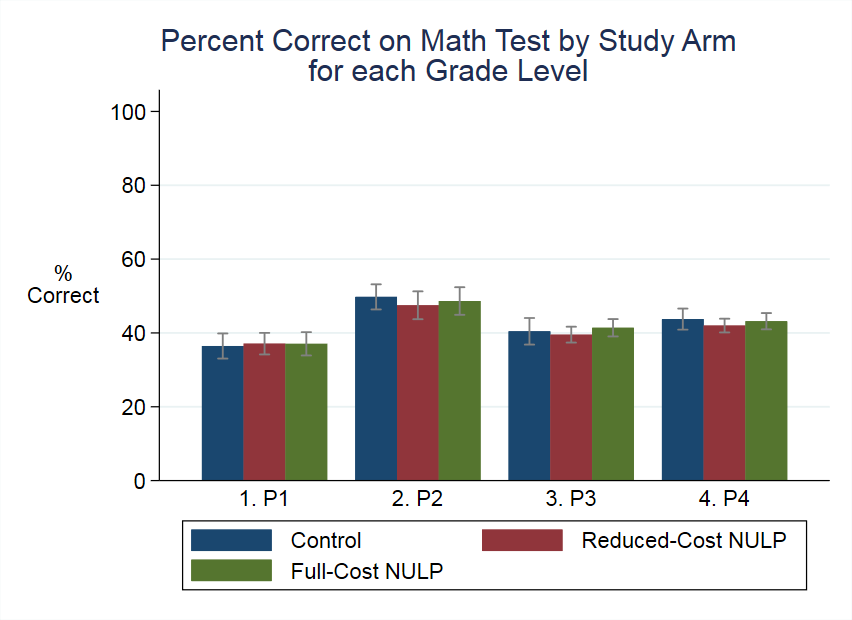
1. Get your results figured out. This is easily the most important part. I make publication-quality tables and figures that are easy to read and tell a clear story. You don’t want to waste time writing up results before you know what they are.
– This is the actual research process. Obviously there is a lot that happens before this, but if you are ready to write a paper then you need results to write about.
2. Figure out your story and write it in 100 words maximum (the AER limit), which is 5 sentences. This is your abstract.
– If you can’t tell your story in 100 words then you don’t have a paper yet. You might have several papers, but most commonly you actually have zero.
3. Present your work to try to convince others of your story. This helps you hammer out what the argument is and nail down the exact results. It is iterative with 1 and 2.
4. Write your story in roughly 15 sentences that outline everything you will do in the paper. These will be the topic sentences for your introduction. (Good intros in applied micro have topic sentences for each intro paragraph, that can be read on their own and also say what the paragraph is about. Your paper has to be designed to be skimmed.)
These should discuss the following points in order (many with more than one sentence apiece):
– What is the research question
– What do you do
– What do you find
– Mechanisms for the results, if relevant
– What does this mean?
– How does this contribute to the literature, i.e. how does it build on what we already know?
Note that first five of these points could also be the five sentences in your abstract. If you have other key things to say then they belong somewhere in the introduction—most likely under “What does this mean?”
5. Fill in the details behind each topic sentence. This is your introduction. I aim for 4 pages but many good recent papers go longer.
– Supreet Kaur’s paper about nominal wage rigidities has a great example of how to write an effective introduction
– More generally, your introduction should emulate the structure of well-published papers in your area—there are plenty of great papers outside the top 5, but top 5 papers are much more likely to have nailed a good introduction
– reviews of the literature should only go into the contributions paragraphs at the end. Do not start with a lit review, no one cares. Do not write a separate lit review section; no one cares. You should integrate citations into your actual argument or leave them out.
– get to your results on page 1.
Writing your introduction is the hardest and most important part of writing the paper. Many people will not read anything else, even conditional on opening the paper. Economics papers are all way too long, and part of the reason is that they include many things that would be in the online methods appendix of a paper in the hard sciences. Our introductions are the equivalent of the entire paper in many disciplines.
– Introductions that use topic sentences for each paragraph and communicate the entirety of the paper are the norm in high-quality economics papers. My understanding is that this is how students are trained to write at Harvard and MIT. Once you start noticing this approach you will see it all over the top econ journals.
While this is an implication of the previous points, I want to state explicitly that your results go in the introduction. Do not tell people that your paper will estimate the effect of X on Y; tell them the effect of X on Y. Definitely do not wait until the last paragraph of the introduction to mention your results.
6. Write the data section of the paper
7. Write the methods section
8. Write up the results. This should be a discussion of what the results mean. Do not include a separate “discussion” section since in that case the results section is pointless.
– Robustness checks go in a subsection here
– Limitations should be acknowledged in here, and also in the introduction where relevant. If they’re major (or if a referee/editor demands it) you can make them a separate subsection.
9. If relevant, write the mechanisms section.
10. Write a conclusion section using Marc Bellemare’s conclusion formula (https://marcfbellemare.com/wordpress/12060). I think conclusions are pointless and shouldn’t exist but since you have to have one, Marc’s approach is the constrained optimum.
– My view is that anything that’s truly important in the conclusion should be in the introduction of the paper. Since many people will not read the conclusion, you should state the key parts in your introduction as well.
That’s it: 10 weeks and you have a paper, and you can easily do a bunch of other stuff on the side at the same time. Now you might say “but Jason, I don’t have my results and story figured out” which might be true. In that case step 1 is going to take longer—but your issue is not finishing the paper, but rather doing the research. The good news in that case is that doing research is fun! So at least you can enjoy it.
This post originated as an email that I sent to a student from another institution that I had a meeting with. I thought it might be helpful to other people as well so I am putting it up where more people can find it.